今回紹介するのは「マルコフ連鎖」というものです。
これは簡単に言えば、今現在からの状態が変化する確率が、これまでの状態がどのようなものであったかに関わらず、現在の状態のみから決定するようなモデルのことをいいます。
つまり、天気で言えば、明日の天気予報が昨日までの天気がなんであったか関係なく、今日の天気がなんであったかで決まるようなものです。
今回はこの「マルコフ連鎖」についての基本的な部分について解説していきます。
確率過程とは
まずはじめに、確率過程とは、「時間の経過などの条件によってランダムに変化していくものを数学的に表したもの」のことを言います。
例1:コイントス
確率の例として同じみコイントスです。
コイントスを何度も繰り返して、表が出たら\(X_i = 1\)、裏が出たら \( X_i = 0 \)として記録していくことも確率過程の一つになります。
ここでいう「コイントスをした回数」が条件になって、それぞれ\( \frac{1}{2} \)の確率で0か1が記録されていることになります。
コイントス以外にも、サイコロで1が出たら\(X_i=1\)、1以外が出たら\(X_i=0\)としたものなども確率過程になります。
特にこれらのような、前回までの結果に左右されない独立な事象の列になっている確率過程をベルヌーイ過程と呼びます。
少し余談になりますが、「1」と記録される確率が\(p\)の試行(コイントスなら\(p = \frac{1}{2}\))を\(n\)回行って、\(X_i = 1\)となった回数が\(k\)回になる確率は、
\(P(k) = {}_n C_k p^k (1-p)^{n-k} \)
で表され、このような確率分布を二項分布と言います。
例2:天気
天気予報でも「明日の降水確率は○○パーセント」と言っていますよね。
明日の天気は、今現在の低気圧・高気圧の位置や気温、風などによって予想しているのだと思いますが、現実問題として明日の天気を正確に言い当てることはできません。
しかしベルヌーイ過程のようにコイントスのように決まるわけでもなく、今現在の天気から明日の天気の確率が算出されているわけです。
このモデルもまた確率過程になっています。
マルコフ過程・マルコフ連鎖
今回のテーマのマルコフ連鎖はマルコフ過程の一種になるので、マルコフ過程の説明を行っていきます。
マルコフ過程とは、過去どのような結果だったかが一切無関係で、今現在の値だけで今後の確率が決定する確率過程のことを言います。
先程例に上げた天気が現実的に見てどうかは置いておいて、下の図は天気がマルコフ過程によって決まるとしたときの一例になっています。
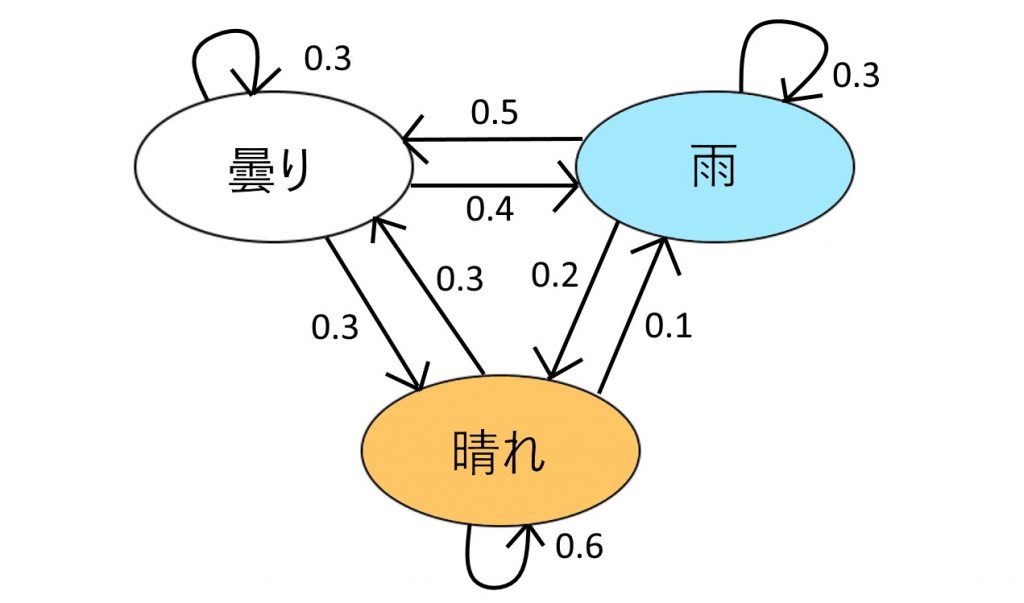
確率は私が適当に決めたものなので現実とは違うと思います。
図の見方としては、それぞれの天気から引いてあるやじるしの隣に書いてある確率が次の日その天気になる確率になっています。
例えば、今日が晴れだったら明日の天気は、
- 60%の確率で晴れ
- 30%の確率で曇り
- 10%の確率で雨
になります。
今回の例は1日ごとの天気という設定で行いました。
これは離散的(値がとびとびになっている)な時間軸上でのマルコフ過程になっていますが、連続する時間軸上でのマルコフ過程も成立します。
天気だとなかなかイメージしづらくなってしまいますが、気温や湿度、風の強さは常に変化しているものなので、今現在の風の強さのみから次の瞬間の風の強さの確率分布がわかる、ということです。
数学的に言うのであれば、時刻\(t\)と十分に微小な時間\( \Delta t\)に対して、時刻\(t + \Delta t\)の風の強さの確率分布が時刻\(t\)の風の強さからのみで決まる(時刻\(t\)以前の風の強さは関係ない)状態のことです。
マルコフ連鎖
そしてついにマルコフ連鎖についてです。
マルコフ連鎖と遷移確率
マルコフ連鎖とは、離散的な時間軸でのマルコフ過程のことを言います。
マルコフ過程の例として提示した天気の例がそのままマルコフ連鎖になっています。
ですので、天気の例を使ってマルコフ連鎖について少し考えていきましょう。

今のところ天気の移り変わりの確率は図に書いてあります。
マルコフ連鎖では、この移り変わりの確率を遷移確率(推移確率)と呼び、すべての遷移確率まとめて遷移確率行列と呼ばれる行列で表します。
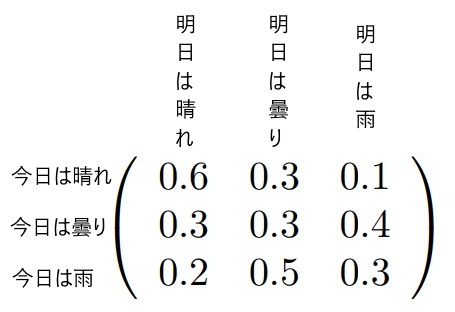
これが上の天気の例の遷移確率行列になっています。
明後日が晴れになる確率は?
天気のマルコフ過程では今日の天気から明日の天気の確率がわかります。
では、明後日の天気はどうなるでしょうか。
マルコフ連鎖であることから、今日から明日についての遷移確率と明日から明後日についての遷移確率は同じものになります。
このことを利用することで、次のような行列の掛け算から今日から明後日への遷移確率行列を求めることができます。

今日が晴れで明後日も晴れる確率を普通に求めようとすると、
- 明日が晴れで明後日も晴れる確率
- 明日は曇りで明後日は晴れる確率
- 明日は雨で明後日は晴れる確率
の3つをそれぞれ求めて足し合わせることになります。
上の遷移確率行列の積を見てみると、
赤で囲まれた部分は、今日が晴れの時の明日の天気の確率
青で囲まれた部分は、明日の天気に対して明後日が晴れになる確率
を表しています。
このそれぞれのベクトルの内積は
- 明日が晴れで明後日も晴れる確率
- 明日は曇りで明後日は晴れる確率
- 明日は雨で明後日は晴れる確率
の和になるので、緑で囲まれた\( 0.47 \)が、今日が晴れで明後日も晴れる確率になっています。
積によって得られた遷移確率行列は、今日の天気に対しての明後日の天気の確率を表しているため、それぞれの天気に対しての確率がわかるようになっています。
そして、2回かけたら2日後の天気の遷移確率行列が得られたように、\(n\)回かければ\(n\)日後の天気の遷移確率行列を得ることができます。
まとめ
今回は「マルコフ連鎖」を紹介しました。
マルコフ連鎖は状態の遷移についての確率モデルになっていて、統計学だけでなく、機械学習の一種である強化学習でも用いられます。
今回天気を例に挙げましたが、現実的な問題としては過去の状態も使って明日の天気は予測されていると思うので、直接的に役立つようなものではないと思いますが。
では今回は以上となります。
最後まで読んでいただきありがとうございました!











コメントを書く