今回扱うのは「高次元」についてです。
私たちが暮らしている世界は3次元の世界なので、見たり、イメージできるのは3次元以下の次元になります。
ところが大学数学では線形代数に始まり、4次元以上のベクトルや空間を扱うことが多々あります。
4次元といえばとあるポケットが有名ではありますが、実際のところ4次元とはどんなものなのでしょうか。
数学で4次元以上を扱う際には基本的には考えすぎずに式として処理していくのが良いとは思いますが、やっぱりイメージできれば理解しやすいですし、高校数学に慣れた状態で高次元に会うのでイメージすることに固執しすぎて理解が進まないこともあるかと思います。
前半は数学的な知識をできる限り使わずに書いているので、数学が苦手な方も前半だけでも読んでみてください。
後半は円・球・4次元以上の球体を用いて、少し数学的な観点から高次元を見てみます。
そもそも2次元・3次元は何か
4次元以上について考えていく前に、まずは私たちがイメージしやすい1次元、2次元、3次元について考えていきましょう。
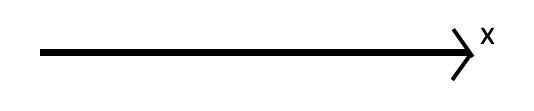
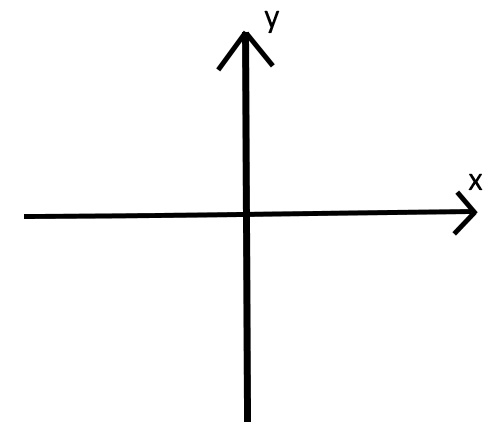
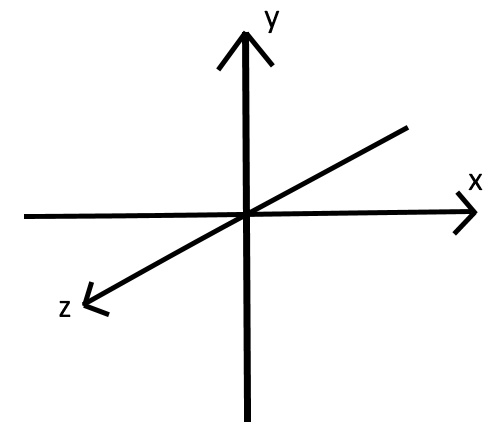
皆さん高校や大学で習っていると思いますが、これらが1次元、2次元、3次元の座標軸です。
当たり前ですが、次元が増えるごとに座標軸が1本触れていきます。
基本的には座標軸同士は直行(垂直)していますが、平行になっていなければ座標軸同士のなす角度は関係なかったりします。
さて、1次元から2次元への変化としては、\( y \)軸方向の座標軸が現れたことにあります。
言い方を変えれば、すべての\(y\)から\(x\)軸が生えているみたいなイメージです。
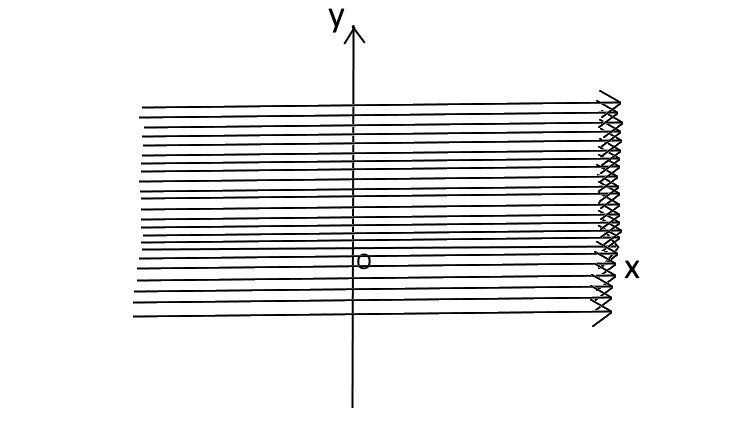
雑に描くとこんなイメージ
この隙間にも無数に\(x\)軸が生えていて、それぞれの\(y\)の値に対して\(x\)の値が存在している感じです。
また、\(y = ax + b\)という1次関数は、\(x\)が変化することによって\(y\)が変化していきますよね。
これは見方を変えると、\(x=k\)に対して\(y=ak +b\)に点が打ってある1次元空間が存在している、ということになり、1次元空間が\(x\)軸上を
そしてこれと同じことが3次元でも起きています。
図にするとさすがに訳が分からなくなりそうなので文章になりますが、\(z\)軸のすべての値に対して2次元平面があるようなイメージです。
じゃあ4次元はどうなるか
4次元以降についても同じように、4つ目の座標軸\(u\)のすべての値に対して3次元空間がある、ということになります。
しかし、私達人間は4次元を視ることができないので、イメージするには少し工夫が必要です。
4次元と聞いてイメージが浮かんだ方は時間と空間、つまり時空間を想像されたんじゃないでしょうか。
空間と時間をセットにしたものが私達人間が最もイメージしやすい4次元だと思います。
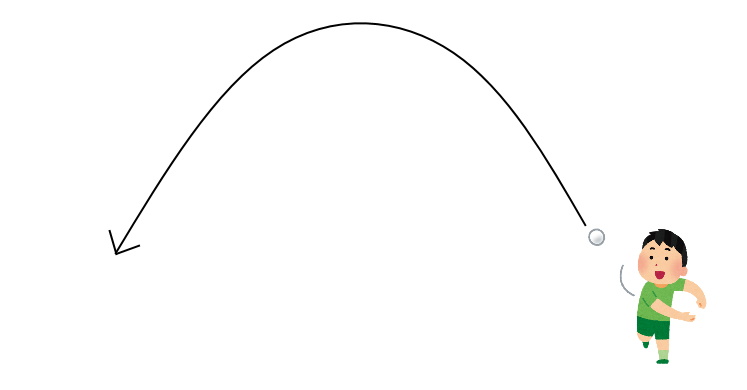
今、目の前に人がいてボールを投げているところを想像してみてください。
時間が経つにつれてボールが移動していきますよね。
これはつまり、それぞれの時間ごとにボールがある場所によって3次元空間が変化していっている、ということになり、
少し見方を変えれば、それぞれの時間ごとにボールのある位置が異なる3次元空間がある、ということになります。
これが4次元の一つの例になります。
まとめると、4つある座標軸のうちの3つで3次元空間をイメージして、それがもう一つの座標軸上を動いている、みたいな感じです。
少しイメージしづらいかもしれませんので、円と球を使って考えていきましょう。
円・球・4次元の球体
円について
まず円についてです。円の方程式はご存じの方も多いと思いますが、下の式です。
\(x^2 + y^2 = 1\)
これは半径1の円の方程式です。
そして、円の内部と円周を表す式は、
\(x^2 + y^2 \leq 1\)
これを\(x\)について解くと、
\( |x| \leq \sqrt{ 1-y^2 }\)
となります。
これは、\(y=k\)では\(x\)は\( -\sqrt{ 1-y^2 } \leq x \leq \sqrt{ 1-y^2 } \)の範囲で動くことができるので、その範囲で線が引かれます。
この作業を\(-1 \leq k \leq1\)の範囲で無限に行っていくと円が完成します。

この性質を逆手にとって、\(y = k\)で引かれた線を頭の中で想像しよう、というのが先ほど述べた4次元を視る方法になります。
今回で言えば、\(k\)を\(-1\)から\(1\)まで動かしていけば、段々と長くなって、長さが2になったところから短くなっていく線をイメージすることができると思います。
球について
3次元の球についても同じようなことができます。
半径1の球の内部の球面を表す式は
\(x^2 + y^2 + z^2 \leq 1\)
で与えられます。これは
\( x^2 + y^2 \leq 1- z^2 \)
と変形することができます。
この式が表すこととしては、\(z = k\)では半径\(\sqrt{1 – k^2}\)の円が描かれているということです。
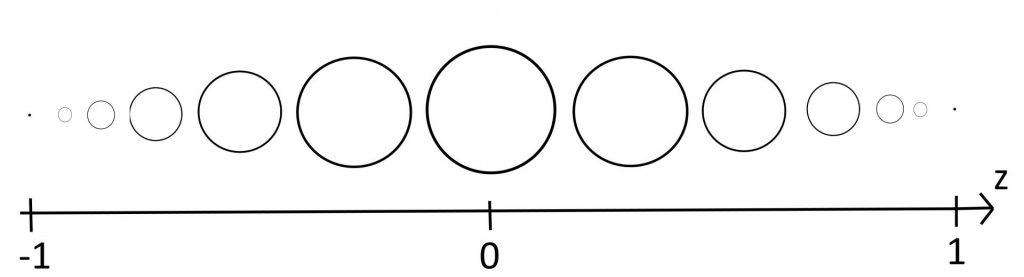
\(z\)軸に対して描かれる円は上の図のようになります。
この図では円が飛び飛びで描かれていますが、実際には\(-1\)から\(1\)まで無限に円が描かれています。
この円を縦に積み重ねていくことで球が完成します。
あと図の円のサイズの比率は適当なのであくまでイメージということでお願いします。
球の場合も先ほどの円の場合と同じように、本来は3次元の球を、\(z\)軸上を動く2次元の図形として捉えることができます。
ここまで少し小難しく数学寄りに考えてきましたが、球に関しては今回の考え方は日常に溢れています。
野菜をスライスすることが一番イメージに近いかなと思います。
例えばスライサーできゅうりを切るところを想像してみてください。
切られて出てくるのは薄く切られた円状のきゅうりです。
これが今回でいうところの円に当たります。
そしてスライスされたきゅうりのそれぞれは元々のきゅうりのどの部分にあったかが決まっていますよね。
これが/(z/)軸の値に当たります。
このスライスされたきゅうりを地道に並べていけば元のきゅうりに戻す(切られてはいますが)ことができます。
これが2次元と3次元の関係性になっています。
4次元の球
2次元の円、3次元の球と見てきたので次はいよいよ4次元の球について考えていきましょう。
円と球の方程式を見ればわかるように、\(n\)次元の球の方程式は\(n\)個の変数の2乗の和と半径によって与えられています。
ですので、半径1の4次元の球の内部と球面を表す式も
\(x^2 + y^2 + z^2 + u^2 \leq 1\)
で与えられます。
これを球の場合と同じように変形すると、
\(x^2 + y^2 + z^2 = 1-u^2\)
となります。
この式が表すこととしては、\(z = k\)では半径\(\sqrt{1 – k^2}\)の球が描かれているということです。
これを球のときと同じように図で表すと、
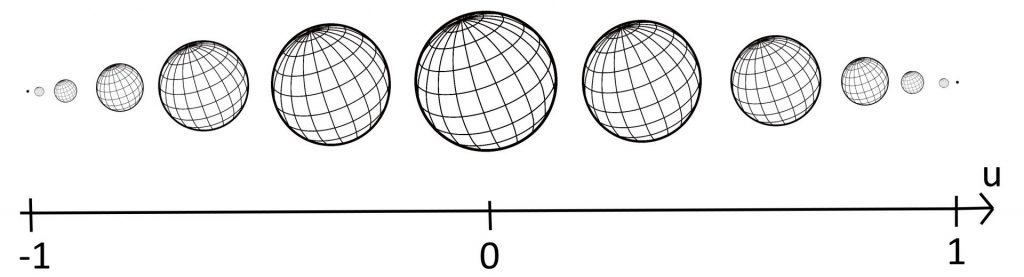
このようになります。
\(u\)軸のそれぞれの値に対して球が描かれています。
つまり、4次元球を1次元座標軸上を動く3次元球として考えられるということです。
まとめ
ここまでを頭の中でイメージできたのであれば、4次元をイメージできるようになったということです!
実際にはパラメータがきれいに分けられるとは限らないので、イメージできない場面も発生しますが、雰囲気は掴んでいただけたかと思います。
今回のことを簡単にまとめると、
\(n\)次元空間は\(n-1\)次元が積み重なってできている
ということです。
これは2次元や3次元についても成り立つことです。
もし4次元以上の空間のイメージに躓いたらこのことを思い出してもう一度考えてみてください。
以前書いたナイトツアーとその高次元化についての記事は今回の高次元に対しての考え方を使っているので、一度読んでいただくと理解がより深まるかと思います。
それでは今回の記事は以上となります。
最後まで読んでいただきありがとうございました!













コメントを書く