お久しぶりです。
前回の更新から半年以上空いてしまいました。
ありがたいことに毎月数百件のアクセスがあり、新しい記事書かないとなぁと思いながら月日が過ぎていました。
最近は勉強のモチベーションが高まっているため、アウトプットの場として使えればと考えています。
さて、今回ですが、パラメータ推定を行う手法の一つである「最尤法」について書いていこうと思います。
現実のデータを扱ってなにかを分析しようとしたとき、
「このデータの母集団は正規分布に従っている」ということがわかっていても、母集団の平均や標準偏差がわからなければ、目の前にあるデータを見ることしかできず、その裏側にある法則を分析することはできません。
そのため、観測値からパラメータを推定する必要が出てきます。
この方法はいくつかありますが、今回はその中でも「尤度」というものを使った、「最尤法」について書いていきたいと思います。
尤度と最尤法
尤度とは
まず、「尤度」とはどんなものでしょうか。
多くの方にとって、尤度という言葉は馴染みのないものかもしれません。
「尤」という漢字は、もっともらしい(尤もらしい)という意味があり、
簡単に言えば、尤度はもっともらしさを表す値になります。
ある分布が、パラメータ\( \theta_1,\theta_2,\cdots,\theta_k \)によって決まるとき、
(例えば、正規分布であれば、平均と標準偏差で分布が定まるので、\( \theta_1=\mu,\theta_2=\sigma \))
観測値\(x=(x_1,x_2,\ldots,x_n)\)の同時確率分布は、\( \theta_1,\theta_2,\ldots,\theta_k \)の関数とみなすことができます。
これが尤度関数\( L( \theta_1,\theta_2,\cdots,\theta_k ) \)です。
数式で書くと、観測値に独立性があれば、この同時確率分布は分布関数の積で表せるので、
$$ L( \theta_1,\theta_2,\cdots,\theta_k ) = \prod_{i=1}^n f(x_i; \theta_1,\theta_2,\cdots,\theta_k ) $$
となります。
「いや、これのどこが尤もらしさだよ!」と思われた方もいらっしゃると思いますので、この積がどんなものなのかを考えてみましょう。
尤度関数って結局何?
簡単に考えるために、分布は標準偏差1の正規分布にしておきます(平均を変数として考えます)。
下の図は、標準正規分布の確率密度関数のグラフです。
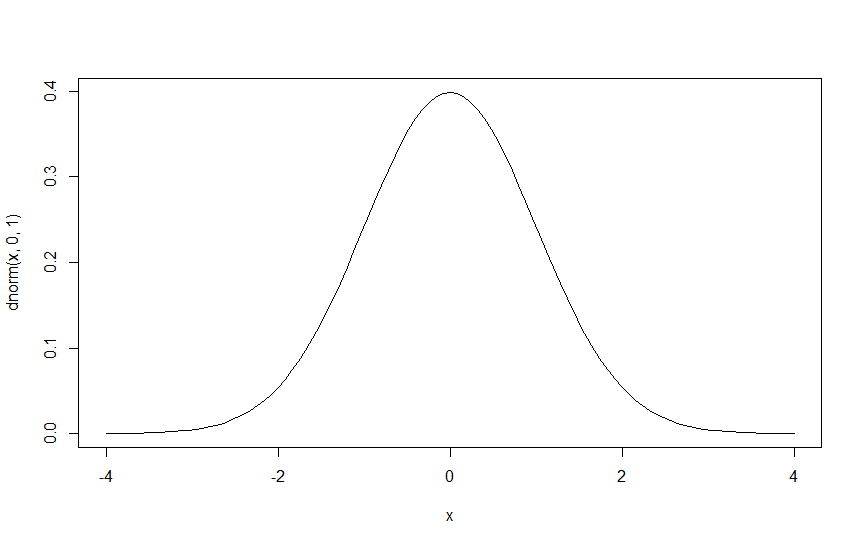
密度関数なので、\(x=0\)が\(f(0)=0.3989423\cdots\)の確率で起こる、というわけではありませんね。
ですが、密度関数が大きな値をとっているところは、小さな値のところに比べて「起こりやすい」、というのは間違いありません。
例:\(-4\)から\(-2\)の値が観測されるよりも、\(-1\)から\(1\)までの値が観測される確率が高い。
ということは、密度関数の値は「起こりやすさ」を表しているわけです。
ここでは\(x\)が変数でしたが、観測値\(x_0=2\)が観測されたとします。
標準正規分布の密度関数\(f(2;\mu=0,\sigma=1)=0.05399097\)なのですが、
平均2,標準偏差1の正規分布について考えてみると、\(f(2;2,1)=0.3989423 \)となります。
標準正規分布では\(x_0=2\)が観測されることはあんまり起こらないけど、
平均2,標準偏差1の正規分布では(x_0=2)が観測されることは、少なくとも標準正規分布よりは起こりそうです。
密度関数の値は「起こりやすさ」を表していたわけですから、\(x_0=2\)が観測値として得られている状況では、母集団の平均が0であるよりも、2である方が密度関数(尤度)の値が大きいので、より「尤もらしい」ということです。
最尤法
これを、観測値すべてについて考え、一番尤もらしいパラメータを探していきましょう、というのが最尤法になります。
尤度関数\( L(\theta_1,\theta_2,\cdots,\theta_k ) \)は積の形をしていて計算するのが大変ですから、多くの場合は対数ととって、対数尤度関数
$$ \log L( \theta_1,\theta_2,\cdots,\theta_k) =\sum_{i=1}^n \log f(x_i; \theta_1,\theta_2,\cdots,\theta_k )$$
を考えます。
$$ \frac{\partial \log L( \theta_1,\theta_2,\cdots,\theta_k)}{\partial \theta_i} $$
をすべての\(i\)について計算し、\(\theta_i\)を求めることで、
観測値が尤もらしくなるパラメータの推定量である最尤推定量を得ることができます。
Rを用いたシミュレーション
ここまでごちゃごちゃと説明してきましたが、ここではRを使って簡単なシミュレーションを行っていきます。
まずは観測値となる値を生成していきましょう。
平均8,標準偏差2の正規分布から32個の乱数を生成させます。
入力
n <- 32 #サンプル数
m <- 8 #平均
sd <- 2 #標準偏差
x <- rnorm(n,m,sd) #乱数生成結果
> x
[1] 7.789528 3.892962 7.142310 8.931339 8.585352 10.307842 7.720405 7.841609 8.114200 8.311233 7.310397
[12] 9.064369 7.112118 6.626315 5.239168 6.690556 7.307140 8.260913 9.474746 8.686918 8.214637 6.384087
[23] 4.154012 9.310105 8.564794 4.520574 6.061854 7.329674 7.629653 10.098268 4.880182 3.911512正規分布における平均と標準偏差の最尤推定量は、
$$ \hat{\mu} = \frac{1}{n}\sum_{i=1}^n x_i $$
$$ \hat{\sigma} = \frac{1}{n}\sum_{i=1}^n (x_i – \hat(\mu) )^2 $$
となる(計算は省略します)ので、
入力
Lm <- sum(x)/n #平均の最尤推定量
Lsd <- sqrt(sum((x-Lm)^2)/n) #標準偏差の最尤推定量結果
> Lm
[1] 7.618652
> Lsd
[1] 2.097836今回、乱数で生成した観測値による平均の最尤推定量は7.62、標準偏差の最尤推定量は2.10であることが分かりました。
確認のため、32個の観測値とこれら最尤推定量をパラメータとする正規分布の確率密度関数をプロットしてみましょう。
入力
curve(dnorm(x,Lm,Lsd), xlim = c(m-4*sd,m+4*sd), ylim = c(0,1/(sqrt(2*pi)*Lsd)+0.05), col=1)
par(new=T)
plot(x,dnorm(x,Lm,Lsd), xlim = c(m-4*sd,m+4*sd), ylim = c(0,1/(sqrt(2*pi)*Lsd)+0.05), col=2)出力
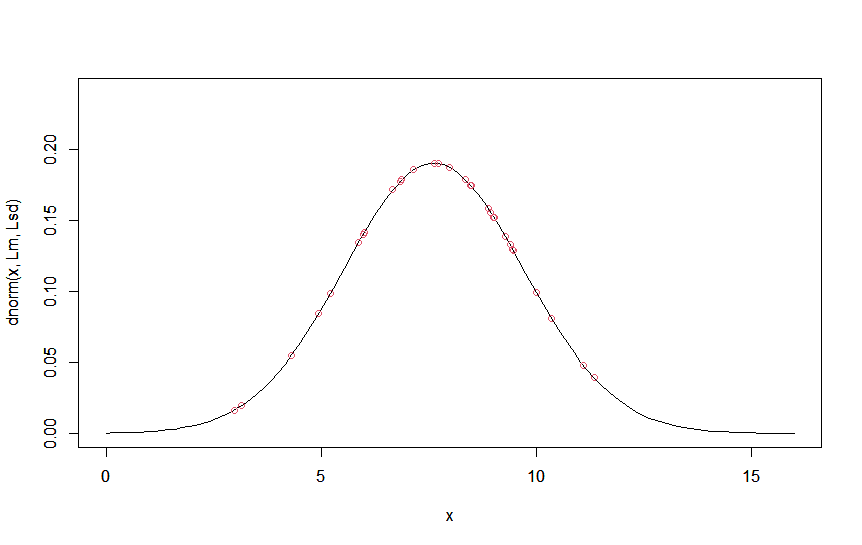
値が\( \hat\mu \)付近に集中していて、いい感じにばらついていますね。
そもそも観測値をどのように生成したかといえば、平均8,標準偏差2の正規分布から32個の乱数を生成したわけでした。
今回得られた最尤推定量は、平均の最尤推定量は7.62、標準偏差の最尤推定量は2.10でしたので、まあまあ推定できていますね。
乱数生成のサンプル数や平均、標準偏差を変えると色々な結果が得られると思いますので、是非試してみてください!
まとめ
今回は、尤度についてRを使ったシミュレーションを使いながら説明しました。
最尤法は、観測値から一番もっともらしいパラメータの値を推測する方法です。
現実のデータがどのような分布から発生したのかを考える際には、分布関数のパラメータの推定が必要になります。
推定の方法には様々な手法がありますが、最尤法はその一つです。
今後は、実データからモデリングを行ったモデルのよさの評価に使われるAIC(赤池情報量基準)や、他のパラメータ推定の手法もご紹介していければと思います。
今回はこれで以上になります。
最後まで読んでいただきありがとうございました!











コメントを書く