今回は以前ご紹介したナイトツアーの高次元化について少し話していこうと思います。
ナイトツアーについてはこちらをどうぞ
ナイトツアーとはそもそもがナイトの駒を使ってチェス盤を移動していく問題ですので、2次元での話になります。
では、ナイトツアーにおける高次元の捉え方とはどのようなものが考えられるでしょう。
3次元のマス目
まずは、視覚的にもイメージしやすい3次元について考えていきましょう。
2次元のマス目が横一列の1次元のマス目を縦に並べたものになっていることと同じように、3次元のマス目は2次元のマス目を積み重ねたものになります。
下の図は8×8×8のマス目のイメージ図で、8×8のマス目が8枚積み重なった形状になっています。

4次元のマス目
3次元のマス目は2次元のマス目を積み重ねることによって作ることができました。
4次元のマス目もこれと同じように考えることができます。
さっそくですが、下の図が8×8×8×8のマス目を表したものになります。
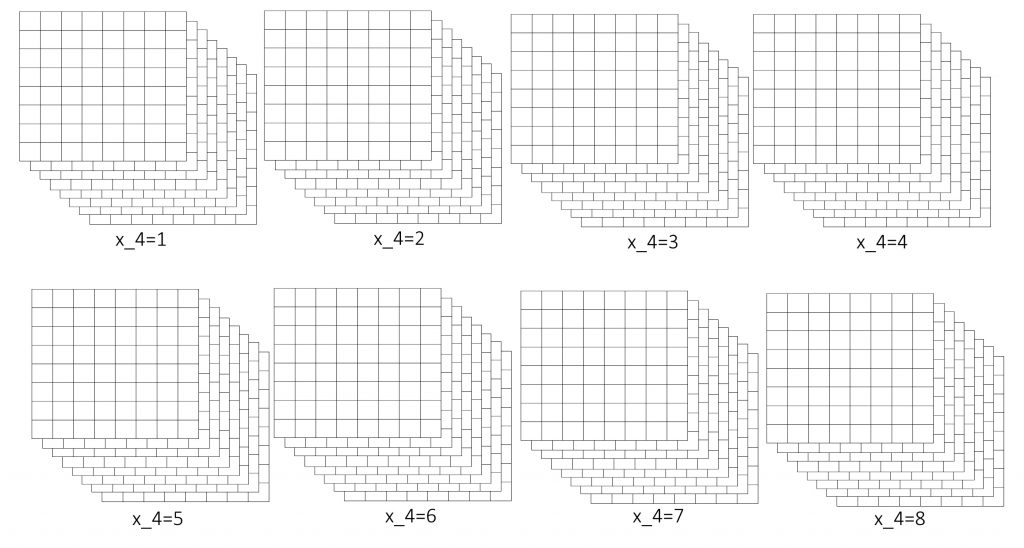
ここからは言葉だけで説明するのも分かりづらくなってしまうので、平面の横と縦が\(x_1,x_2\)軸、先ほどの3次元のマス目で縦に積み上げた方向を\(x_3\)軸とします。
3次元は2次元のマス目を\(x_3\)軸方向に積み上げてできたわけですから、4次元のマス目についても新たに\(x_4\)軸を設定してその方向に3次元のマス目を並べていけば作ることができます。
5次元以上のマス目
5次元以上については図で表すとごちゃごちゃしてしまうので簡単な説明だけに留めます。
5次元以上についてもこれまでの拡張と同じようにマス目を作っていくことができます。
\(n\)次元のマス目に対して、それを\(x_{n+1}\)軸方向に並べていくことで\(n+1\)次元のマス目を作ることができます。
高次元でのナイトの動き(簡単ver)
本来ナイトの駒は2次元平面上を動く駒ですから、高次元でのナイトの動きを定義する必要があります。
ここでは2種類の動き方が考えられるかと思います。
まず1つ目は、いずれかの座標軸方向に1マス、その座標軸以外の座標軸方向に2マス移動する方法です。
2次元のナイトは縦横いずれかに2マス、そこから垂直方向に1マス移動する駒でした。この動き方をそのまま高次元に当てはめた形になります。
下の図は3次元のナイトの動きを表したものになっています。真ん中の段の平面の真ん中にナイトがいて、そこから一般的な2次元のナイトの動きで移動できるのが赤色に塗られたマス目です。
そして、1マス移動する方向を\(x_3\)軸方向、そこからその平面上で縦横いずれかに2マス移動したのが青色に塗られているマス目です。
最後に、2マス移動する方向を\(x_3\)軸方向、そこからその平面上で縦横いずれかに1マス移動してのが緑色に塗られているマス目です。
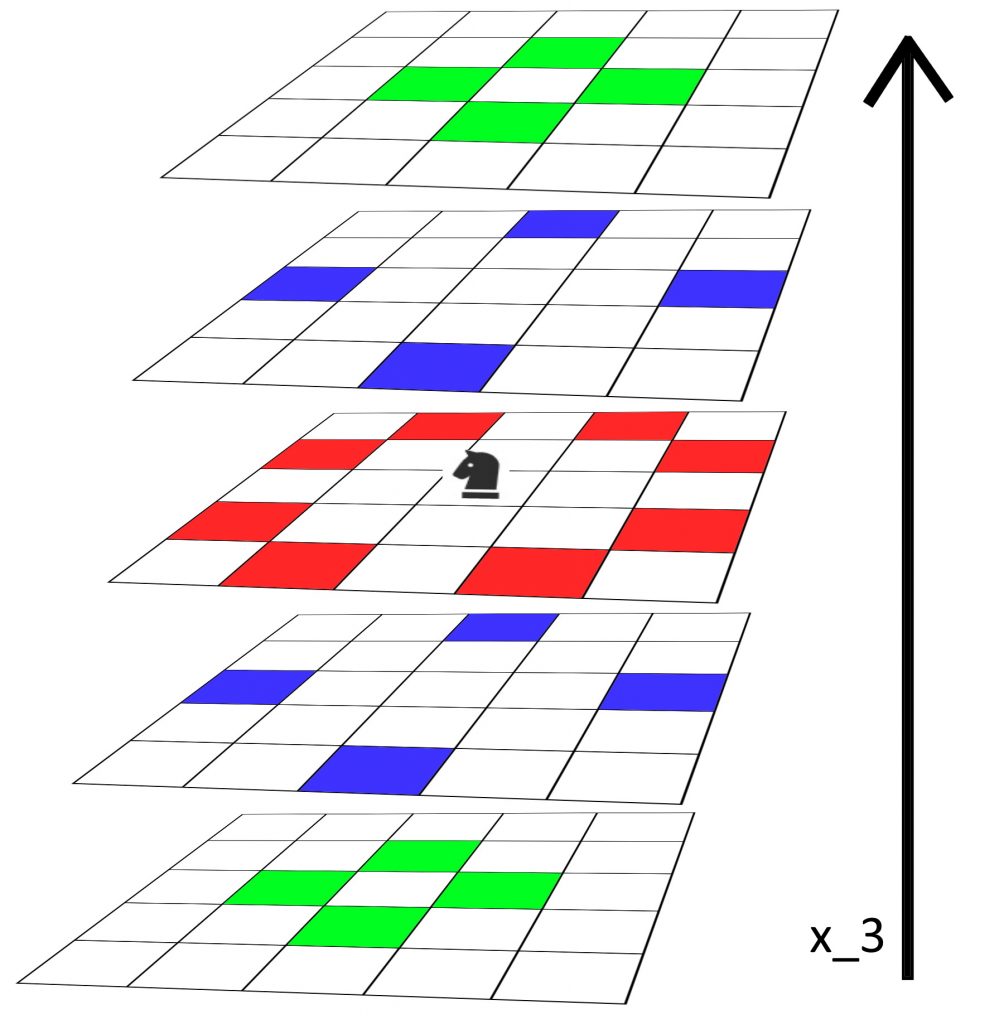
今回扱う高次元ナイトツアーはこの移動方法のものになっています。次に提案する移動方法はこの移動方法よりも問題が複雑になるため、タイトルにもあるように簡単verとしてあります。
高次元でのナイトの動き(難しいver)
ナイトの動きの特徴は単純な斜め移動というだけでなく、1方向に2マス移動するというところにあると思います。
ですので難しいverはその特徴をより活かしたものになっています。
難しいverは、いずれかの座標軸方向に2マス、それ以外すべての座標軸方向に1マス移動する方法です。
下の図は先ほどと同様にこの移動方法で移動できるマス目を色をつけて塗ったものになっています。
2マス移動する方向を\(x_3\)軸方向、そこからその平面上で縦横どちらにも1マス移動したのが青色に塗られているマス目です。
2マス移動する方向を\(x_1,x_2\)軸方向いずれか、そこから\(x_1,x_2\)のうち2マス移動しない方と\(x_3\)軸方向に1マス移動するのが赤色に塗られているマス目です。
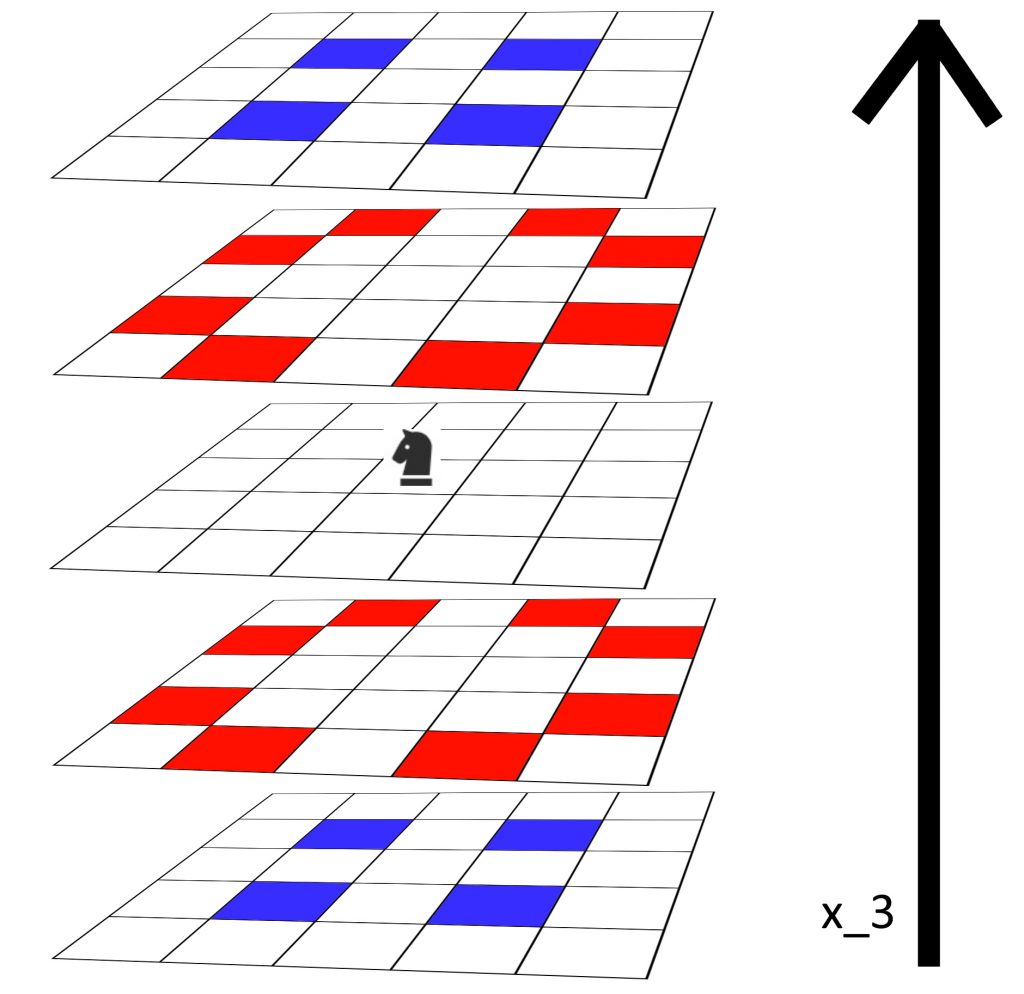
この移動方法が複雑になる要因として、移動するたびにすべての座標軸方向に対して移動しなければならない点が挙げられます。
簡単verの方は平面上での移動も可能になるのでイメージしやすいのですが、こちらは頭でイメージして考えるのが難しく、そもそもナイトツアーを見つけるのも手間がかかります。
ですので今回は簡単verの方だけに話を絞らせていただきます。
あとそもそも難しいverについてはまだあまり考察もできていないので、後日にはなりますがいずれ書きたいと思っています。
高次元のナイトツアー
高次元でのナイトの動きについての定義を行ったところで、ここからは実際に簡単verのナイトの動きを用いた高次元のナイトツアーについて考えていきたいと思います。
2次元のナイトツアーはどのようなマス目がナイトツアーを持っていたかというと、\(n\geq 5\)のとき\(n\times n\)のマス目はナイトツアーを持って、\(n\leq 4\)のときナイトツアーを持ちませんでした。
高次元化した結果として特徴的なものとして、4×4×4のマス目がナイトツアーを持つということにあります。
4×4のマス目はナイトツアーを持ちませんでしたが、次元を拡張したことで移動の制限に余裕ができ、全てのマス目を通過することができるようになりました。
下の図は4×4×4のナイトツアーの一例になってます。
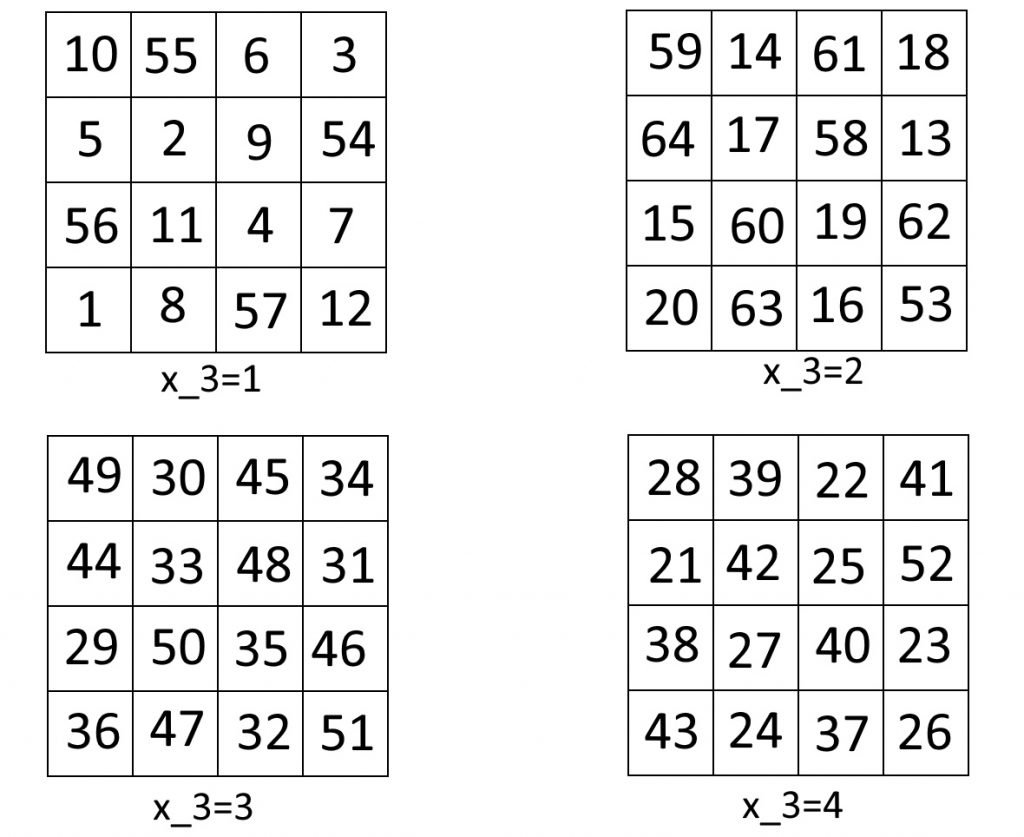
余談ですが、このナイトツアーはナイトが最後に着いたマス目、つまり上の図で64と書いてあるマス目から、最初にいた、1と書かれているマス目に移動することができます。
グラフ理論ではこのような順路は閉じていると言われ、すべての頂点(ここではマス目)をたった一度だけ通って最後にスタート位置に戻ってこれるような順路のことをハミルトン閉路と言います。
ハミルトン閉路の話はナイトツアーを紹介した記事で軽く触れていました。8×8のマス目でのナイトツアーではスタート位置に戻ってこれるようなナイトツアーはないよ、という部分です。
これはつまるところ、「8×8のマス目はナイトツアーにおいてハミルトン閉路を持たない」ということを言っています。
そして、「偶数×偶数のマス目は絶対にハミルトン閉路を持たない」ということでもありました。
これが3次元になったことで偶数×偶数×偶数のマス目がハミルトン閉路を持てるようになったというのは大きな変化だと言えると思います。
少し長くなってしまいましたが本題に戻ります。
2次元の4×4の場合とは異なり、3次元の4×4×4のマス目がナイトツアーを持つことが分かりました。
その一方で、3×3×3や4次元以上の\(3^n\)のマス目については2次元の場合と同様に中心にあるマス目への移動ができないことからナイトツアーを持ちません。
ここまでのことから、\(n \geq 3\)に対して、1辺\(m\)の\(n\)次元のマス目\(m^n\)は\(m \geq 4\)のときナイトツアーを持つ、ということが予想されます。
ではこれをどのように証明するかの概要を軽くお話します。
5×5×5を例にすると、
まず、5×5のマス目に対して次のようなナイトツアーを見つけたとします。
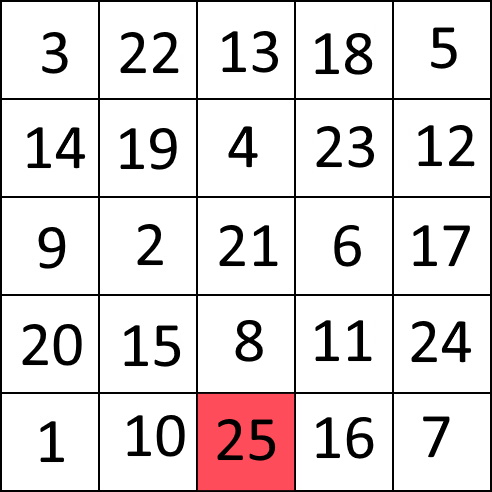
このナイトツアーの最後に到着したマス目はスタート位置の2マス右になっています。
5×5×5のマス目は5×5のマス目を5枚重ね合わせたものだったので、この25手目の位置から一つ隣の5×5のマス目の角に移動することができます。
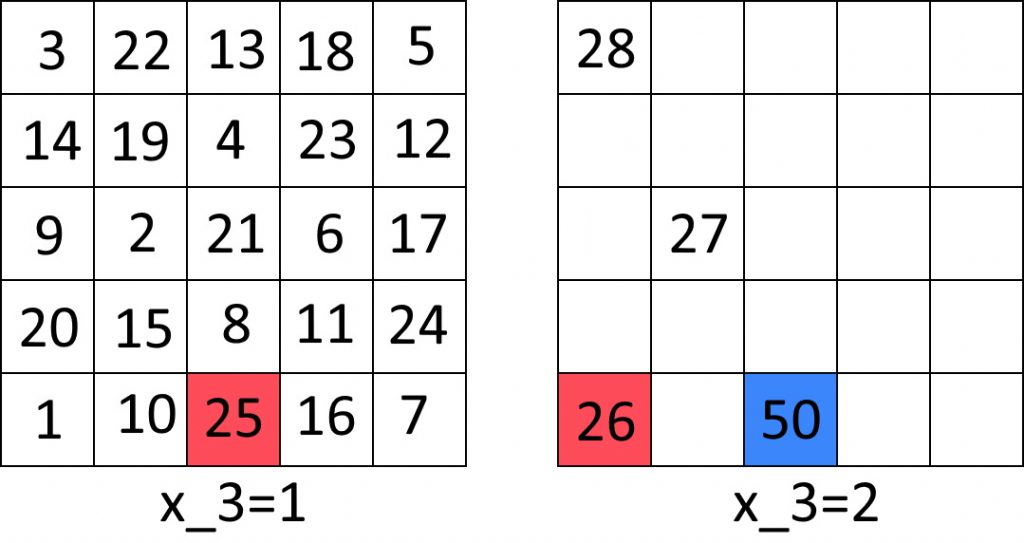
そして1枚目の5×5の1手目にあたる位置の26手目を置くことができるので、ここから1枚目と同じ動き方をして、50手目には先程と同じように26手目の2マス右に着くことができます。
この流れを5枚分すべてに行うことで、5×5×5のナイトツアーを完成させることができます。
そしてこれは4次元以上の場合についても同様のことを行うことができるため、\(n \geq 2 \)に対して\(5^n\)のマス目はナイトツアーを持つということを言うことができます。
これを6×6以降に対しても行っていけば、\(n \geq 3\)に対して、1辺\(m\)の\(n\)次元のマス目\(m^n\)は\(m \geq 4\)のときナイトツアーを持つことを証明できるのですが、すべてのサイズのマス目に対して人力で見つけていくことは不可能なので、数学的に示す必要がでてきます。
これは2次元のナイトツアーについて書いた記事で省略した、5×5以上のマス目についてはナイトツアーを完成させることができることの証明と同時に行うことができるのですが、詳しくは今回も省略させてください。
とはいえそれではモヤっとする方もいらっしゃると思うので、概要だけ書いておきます。
証明の概要
11×11を例にすると、このマス目は下の図のように赤色の6×6、黄色の5×5、青色の5×6が2つの計4つのマス目に分割することができます。
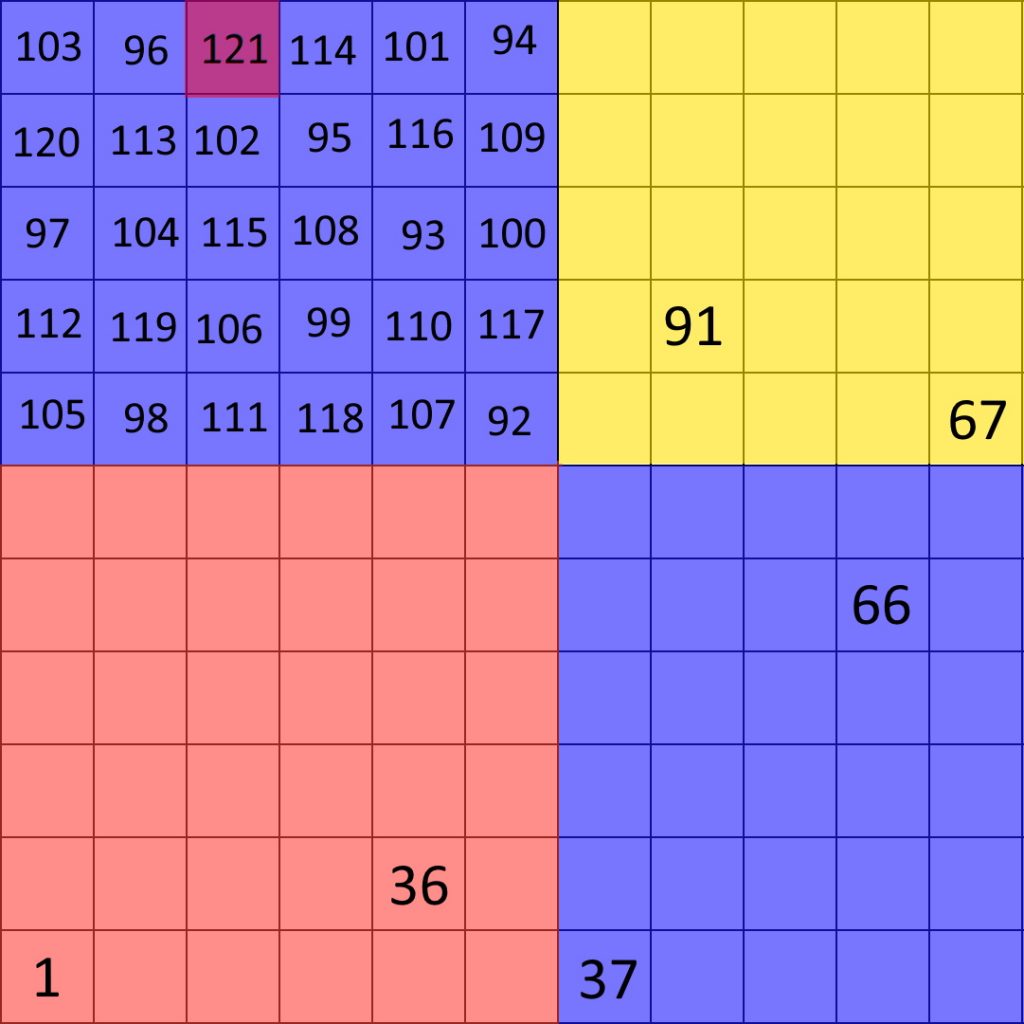
まずこれによって1辺11マスのマス目については2次元以上のときナイトツアーを持つことが分かります。
ここで最後に到着したマス目のある6×5のマス目内でのナイトツアーを次のように、左上の角から1マス内側に入ったところで終了するようなナイトツアーを見つけます。
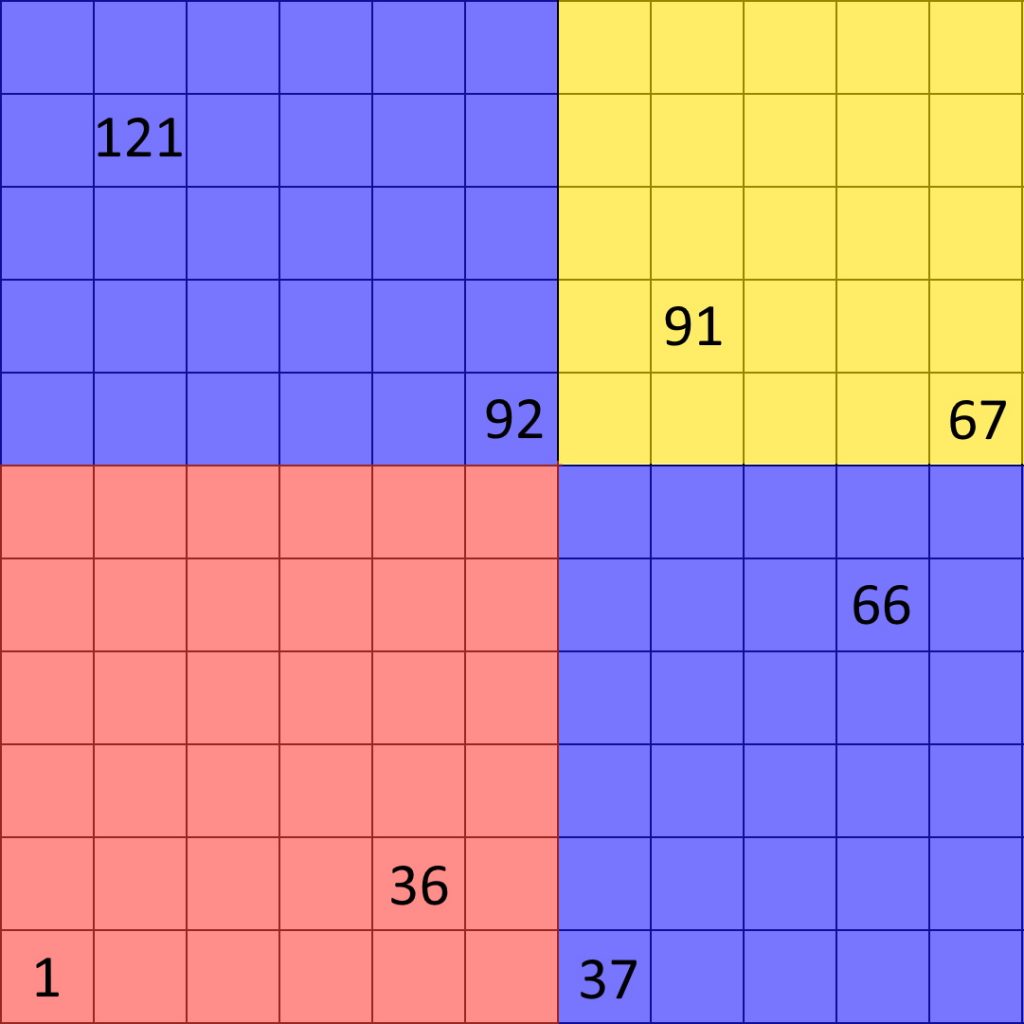
ここで、16×16のマス目は11×11のマス目、5×5のマス目、5×11のマス目2つに分割することができます。
11×11のときと同じようにナイトツアー同士をつなげていくと、
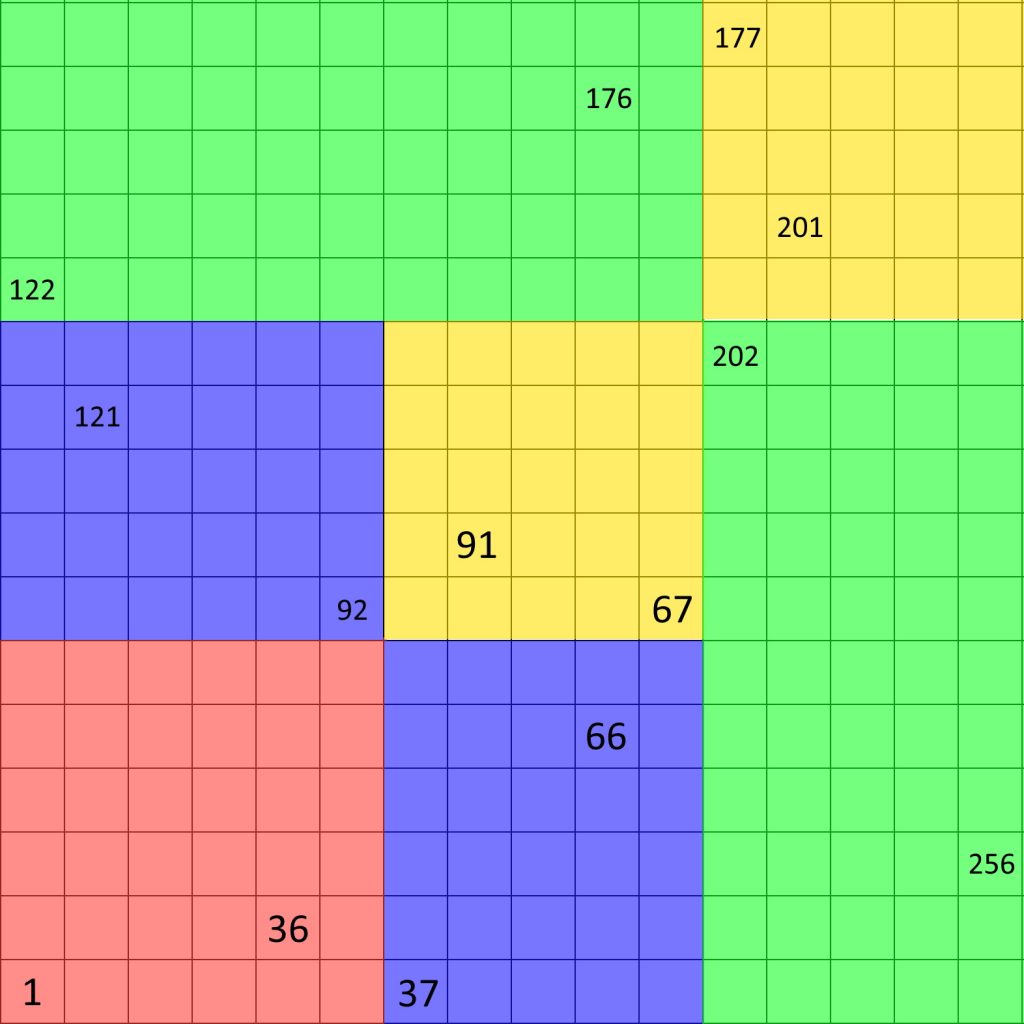
上の図のようになります。
これによって1辺16マスのマス目も2次元以上でナイトツアーを持つことが分かります。
これを繰り返していけば、1辺\(5n+1\)のマス目が2次元以上でナイトツアーを持つことが分かります。
これを\(5n,5n+2,5n+3,5n-1\)についても行っていけば示すことができます。
また、さらっと流していますが、長方形のナイトツアーについても5×5のマス目を使ってナイトツアーをつなげて作ることができます。
まとめ
今回はナイトの動きとマス目を高次元化して、そこでのナイトツアーについて考えていきました。
ナイトの動きは2種類考えられ、今回はそのうち簡単な方についての扱いました。
そして、簡単verのナイトの動きでは、\(n \geq 4\)のとき、1辺\(n\)マスのマス目は3次元以上のマス目でナイトツアーを持つことになります。
今回はこれで以上になります。
ナイトツアーとグラフのことばかり書いてしまっているのでなにか別の話題について書いていきたいですね
最後まで読んでいただきありがとうございます!
次回もよろしくお願いします!









コメントを書く