今回は「グラフ理論」について解説していきたいと思います。
前回紹介したナイトツアーはこのグラフ理論というものの問題の一つであり、今後もグラフ理論に関係することを書いていきたいということもあり、今回紹介することにしました。
グラフ理論というのは、簡単に言えば点と線をつないでできたグラフというものを扱う分野です。
グラフ自体は、電車やバスの路線図だったり、映画とかドラマの人物相関図のように、割と身近な存在ですので、イメージしやすい分野だと思いますので、是非最後まで読んでいただければ幸いです。
グラフとは
冒頭でグラフは点と線をつないでできたものと書きました。
厳密には、グラフ理論の言葉では、線のことを辺、点のことはそのまま点であったり、頂点と言ったりします。
冒頭で例に出した路線図や人物相関図と見比べると下の表のようになります。
| グラフ理論 | 路線図 | 人物相関図 |
| 頂点 | 駅 | 人物 |
| 辺 | 線路 | 人物の繋がり |
下の図は頂点が6個、辺が6本あるグラフの一例です。
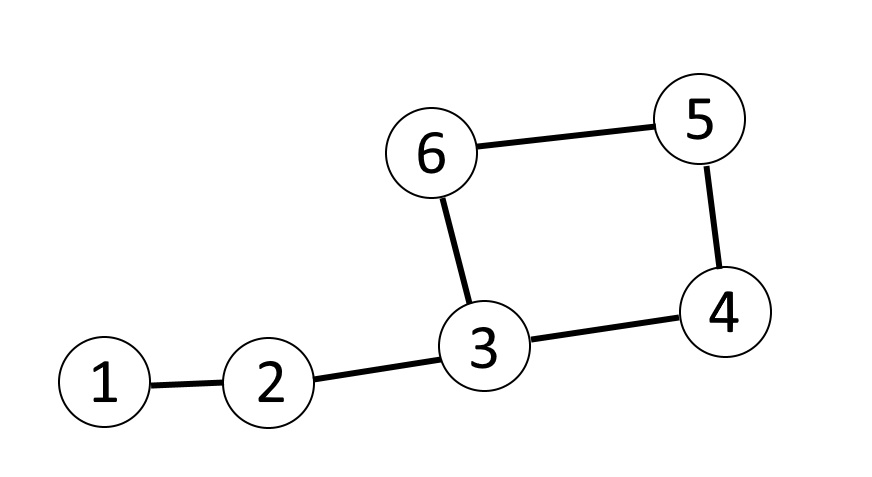
このグラフの名前をGとすると、グラフ理論でよく用いられる表現としては、
頂点の集合\(V=\{ 1,2,3,4,5,6 \}\)
辺の集合\( E=\{ (1,2),(2,3),(3,4),(4,5),(5,6),(3,6) \} \)
グラフ\( G = (E,V)\)
といった表記になります。
ここで、\( E \subset V \)となります。
まず、頂点の集合には頂点それぞれの名前が入り、辺の集合には辺が繋がっている頂点2つを入れた集合が入ります。そして、それら2つの集合を合わせてものがグラフGを表している、ということです。
辺・頂点について
ここでは、グラフ\( G=(E,V) \)について話していきます。
・位数\( |G| \):グラフにある頂点の数
・\( || G || \):グラフにある辺の数
・\( |G|=|E| \)
・\( || G || = |V| \)
・頂点\( x,y\)が隣接:\( (x,y)\in V \)、頂点\(x,y\)が辺で繋がっている
・頂点\(x,y\)が辺\(e\)で隣接しているとき、\(x,y\)は辺\(e\)の端点である、ともいいます。
・辺\(e\)が頂点\(v\)に接続:頂点\(v\)が辺\(e\)の端点
・頂点\(v\)の次数\(d(v)\):\(v\)から接続している辺の数
辺や頂点については言葉の定義がたくさんあり、結構ごちゃごちゃしていますが、ひとまずこれだけあれば足りるかなと思います。
ナイトツアーとグラフ
ここまでグラフについて説明してきましたが、実際にグラフはどのような扱われ方をしているのかを少し紹介していこうと思います。
当サイトの初投稿の記事であるナイトツアーはグラフ理論の問題としては古典的な問題になります。
ナイトツアーがどんなものかについてはこちらを御覧ください!
3×3のマス目はナイトツアーを完成させるような順路は存在しません。これは割と当たり前な話で、真ん中のマスから移動できるマスが存在せず、また、逆に真ん中のマスに行けるマスも存在しない、ということでした。
ナイトは、今いるマス目から移動できるマス目が決まっているため、マス目に番号をつけ、行き来できるマス目同士を線でつないであげることで、下の図のようなものが完成します。

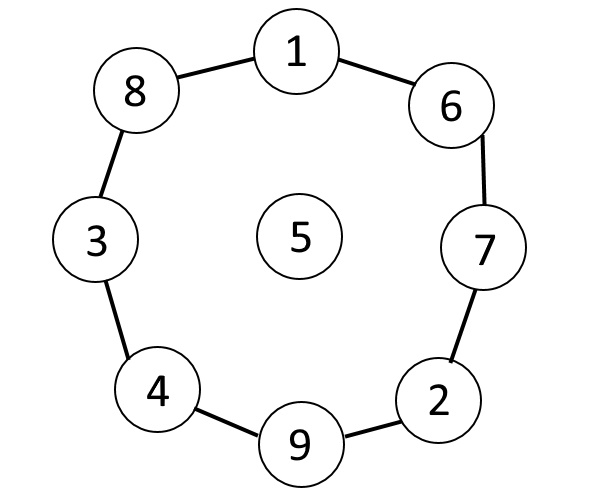
これはグラフになっていて、ぱっと見で5番のマス目には行き来ができないことがわかると思います。
このような視覚化はグラフの良さの一つだと思います。
ネットワーク分析
グラフを用いている分野の一つにネットワークというものがあります。
言葉自体は皆さん聞いたことはあると思いますし、ネットワークを使ってこのサイトに訪れていただいているかと思います。
ここでいうネットワークはグラフそのものだと考えていただいて構いません。
ネットワーク分析では、頂点間の辺による繋がりから、頂点同士の関係や対象となっているものの性質を分析していきます。
例えば、Aさんという人がいたとして、その人と友達になっているアカウントとその周辺のアカウントを、友達関係になっているアカウント同士を辺で繋いで描画したものが下の図だとします。
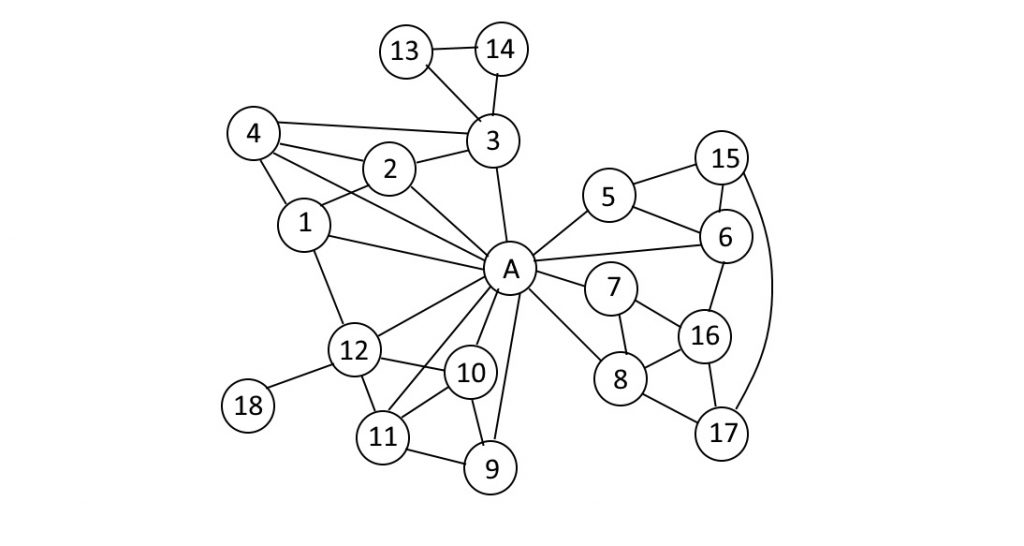
複数のアカウントを使い分けることのできるTwitterなどでは話がややこしくなってしまうので、Facebookなどの実名SNSでの話とします。
実名のSNSではこれまでAさんが関わっている人と友達になっていくため、学生時代の友人、仕事関係での友人、趣味での友人など、さまざまなコミュニティ上での人たちと友達になっていくことになります。
そして、例えば学生時代の友人であればその友人同士がSNS上で知り合いになっているケースは多いと思いますし、それぞれのコミュニティについても同じようなことが起こりますよね。
つまり何が起こるかというと、横の繋がりがある人たちをまとめていくと、人の関係をグループ分けできるということです。
グループをどのように分けるかは様々な方法があるのですが、とりあえず難しいことを考えずに私が感覚的にグループ分けをしてみました。
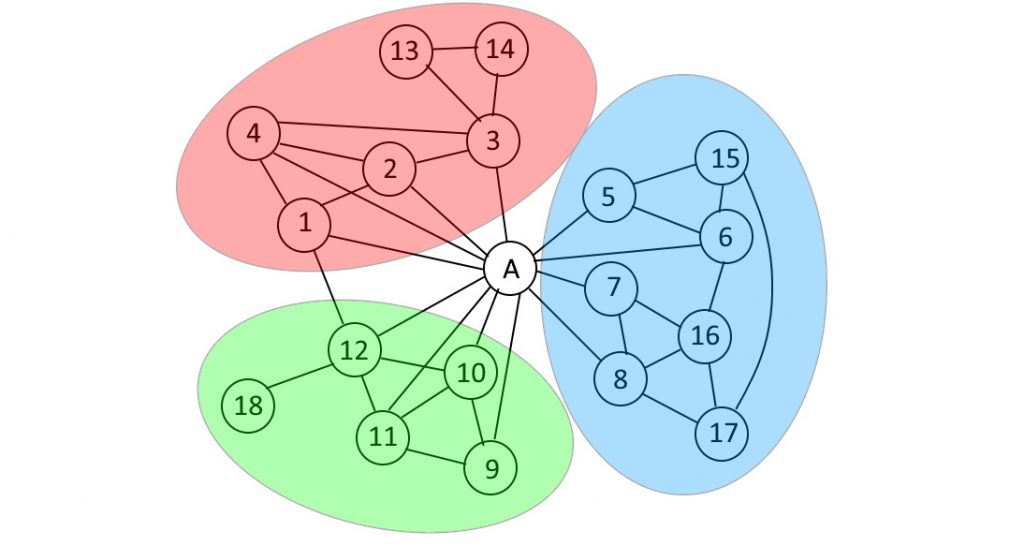
おそらく皆さんもイメージしやすいのはこのようなグループ分けかなと思います。
しかし、1番と12番が友達になっていることから、
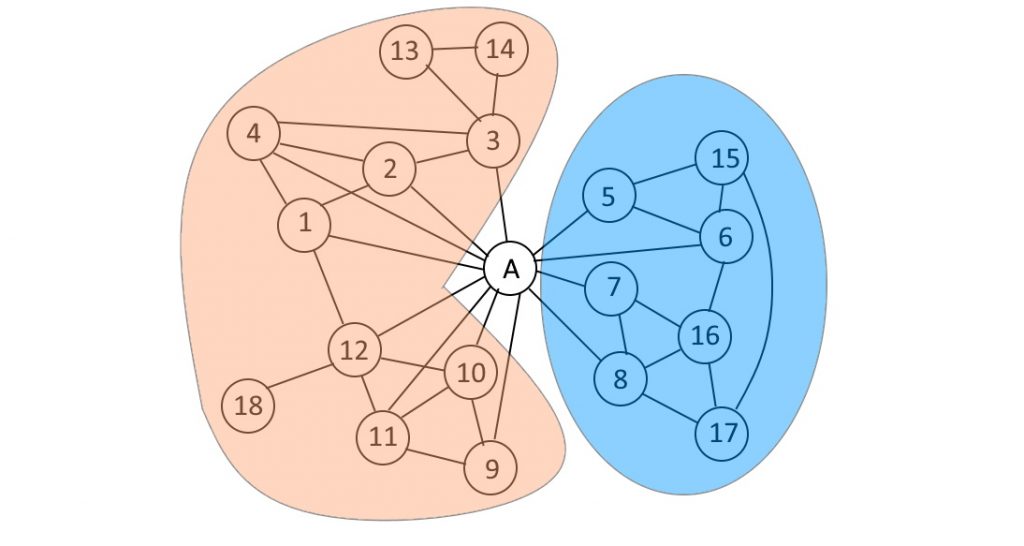
このような分け方をすることもできそうですよね。
このグループ分けはネットワーククラスタリングと呼ばれるもので、どのような基準でグループ分けするか、そしてそのグループ分けが何を基準に正しいといえるのか、について様々な手法が提案されています。
グラフ理論を勉強するのにおすすめの本
私がグラフ理論を勉強するのに使った本をご紹介します。
まず、簡単めな方は、
こちらの情報科学のためのグラフ理論です。
「情報科学のための」とあるように、がっつりとグラフ理論をやりたい!って方には向かないかもしれませんが、必要なことがコンパクトにまとまっている印象です。
続いて2冊目は、
シュプリンガーのグラフ理論です。
Amanonは2000年のものになっていますが、
2012年に再出版されており、その際の定価は4200円+税ですのでご注意ください。
全体で380ページ程とページ数もあり、グラフ理論をしっかり勉強したい方にとって必要な情報はまとまっていると思います。
また、私自身は読んだことはありませんが、以下の2冊は評判も良いのでよさそうです。
まとめ
もちろんこれら以外にもグラフ理論の使い道はあります。
目的地までの最短経路を教えてくれるカーナビや地図アプリも重み付きグラフというものを使って考えられていたりします。
個人的にはグラフ理論が好きなので、今後も色々な記事を書いていきたいと考えています。
今回はこれで以上になります。
最後まで読んでいただきありがとうございました!













コメントを書く